Portfolio item number 1
Published:
Short description of portfolio item number 1
Published:
Short description of portfolio item number 1
Published:
Short description of portfolio item number 2 
Published in Frontiers in Systems Neuroscience, 2018
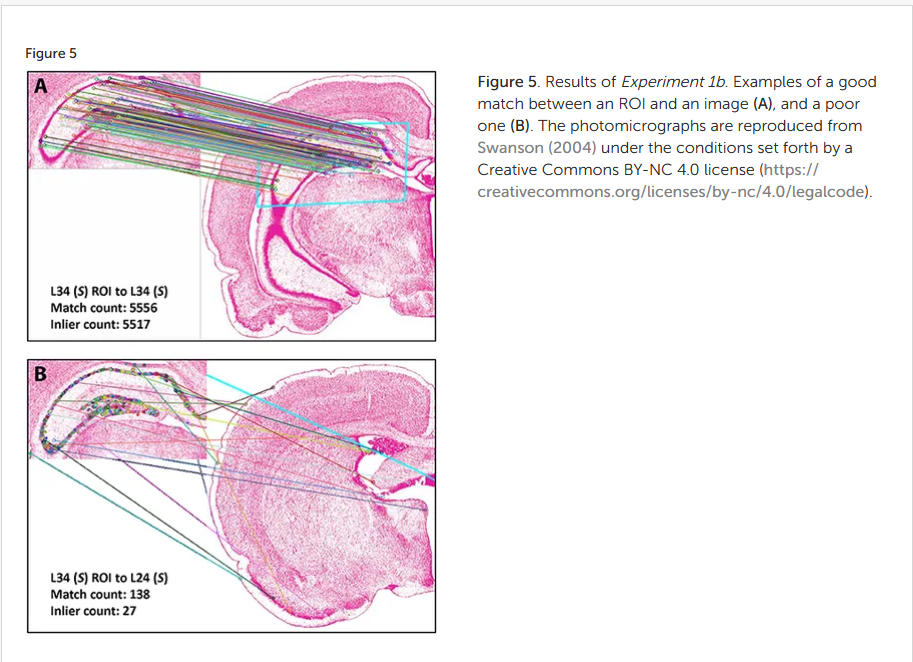
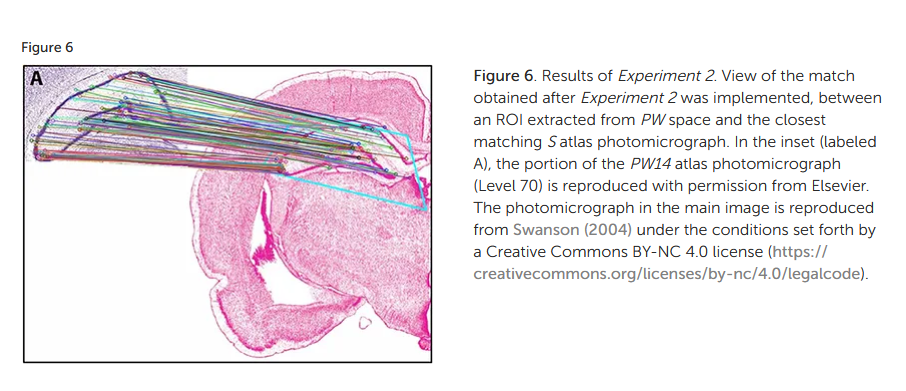
Recommended citation: A. Khan, J. Perez, and O. Fuentes, “Computer vision evidence supporting craniometric alignment of rat brain atlases to streamline expert-guided, first-order migration of hypothalamic spatial datasets. Frontiers in System Neuroscience, 2018.
Download Paper
Published in Proceedings of SPIE Defense + Commercial Sensing Symposium, 2021
In many real-world multi-domain applications, if there is an opportunity to sense the opponent’s strategy from previous rounds, an agent can exploit its opponent in payoffs by playing a specific Best Response (BR) strategy. The optimal way to exploit the opponents in such contests is to learn specific BR strategies for each candidate’s strategies. However, in a large strategy space, learning BR policies for all the strategies is infeasible. We need to find a reasonable point to learn some BR strategies to exploit the opponent strategies, which motivates us to propose a novel method for finding better agent strategies while facing a specific set of opponents in repeated games. Our method is called Clustered Double Oracle Empirical Game-Theoretic Analysis (CDO-EGTA), which builds upon the classic Double Oracle (DO) framework based on Deep Q-Network (DQN) and clustering methods. Empirical results show that our method outperforms the current state-of-the-art methods in terms of regret.
Recommended citation: M. Porag, J. Perez, C. Kiekintveld, T. Son, W. Yeoh, E. Pontelli, "Empirical Game-Theoretic Methods to Minimize Regret Against Specific Opponents". Proceedings of SPIE Defense + Commercial Sensing Symposium, 2021.
Download Paper
Published in Proceedings of the ASME 2022 Fluids Engineering Division Summer Meeting, 2022
Physics Informed Neural Networks (PINNs) provide a way to apply deep learning to train a network using data and governing differential equations that control the physical behavior of a system. In this text, we propose using the PINNs framework to solve an inverse problem which will discover the partial differential equations for compressible flow from Mach number = 5 by coupling Navier Stokes Equations with a Deep Neural Network (DNN) based on training data generated by a CFD solver. The equations of momentum in 2-dimensions and the equation of energy will be parametrized to let Neural Networks calculate two established learnable parameters. This paper will focus on capturing physics governed by fluid flow phenomena applied to high-speed flows using PINNs, which will allow us to see disturbances such as a shock wave interaction with the free stream. Subsequently, a quantification of the predicted results of PINNs will be carried out, and it will be determined if PINNs are computationally less expensive than the Spectral Element Method codes so widely used.
Recommended citation: D. Villanueva, B. Paez, A. Rodriguez, A. Chattopadhyay, V.M. Kotteda, R. Baez, J. Perez, J. Terrazas, V. Kumar, "Field Predictions of Hypersonic Cones Using Physics-Informed Neural Networks". Proceedings of the ASME 2022 Fluids Engineering Division Summer Meeting, 2022.
Download Paper
Published in Proceedings of the ASME 2022 Fluids Engineering Division Summer Meeting, 2022
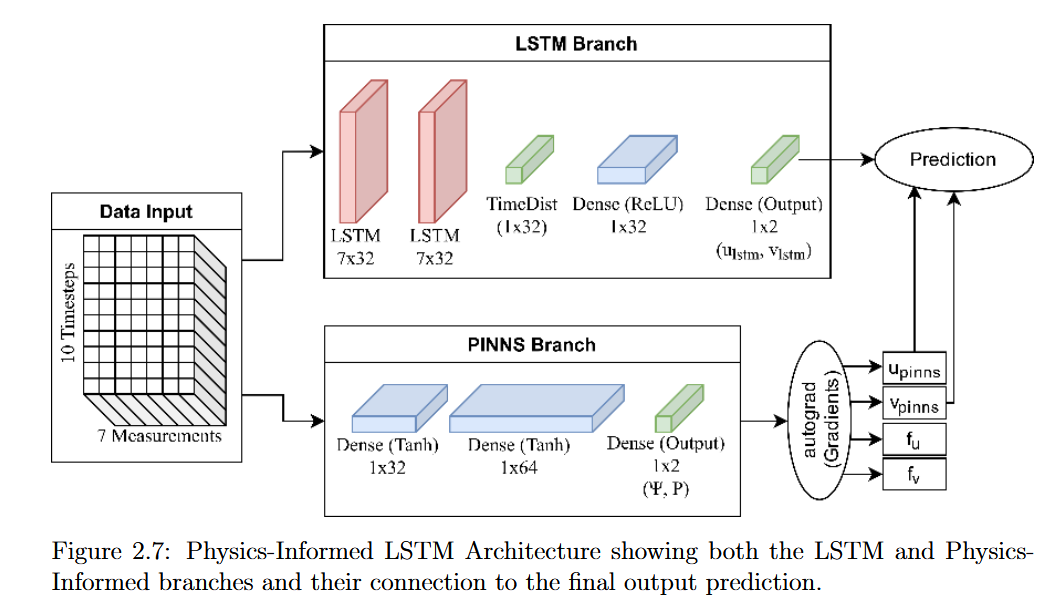
Recommended citation: J. Perez, R. Baez, J. Terrazas, A. Rodriguez, D. Villanueva, B. Paez, A. Cruz, O. Fuentes, V. Kumar, "Physics-Informed Long-Short Term Memory Neural Network Performance on Holloman High-Speed Test Track Sled Study". Proceedings of the ASME 2022 Fluids Engineering Division Summer Meeting, 2022.
Download Paper | Download Slides
Published in , 2024
Deep neural network models are state-of-the-art for many image, audio, text, and video processing problems in different fields of study and disciplines. However, training many of these networks can require a lot of data and gathering such data can be time consuming, costly, and difficult to set-up. This limiting factor can prevent researchers and engineers that do not have access to a lot of resources from using all the tools and models available in deep learning to tackle novel problems in their respective fields. To work around these data limitations, many techniques and models in the field of Few-Shot Learning have been proposed over the years in the sub-fields of transfer learning, data augmentation, and meta learning. One such model, Physics-Informed Neural Networks or PINNs, relies on the fact that datasets collected in the real world must follow the laws of physics, allowing us to leverage our knowledge of physics to help improve performance on these datasets without requiring more data to be gathered. I propose 4 ways of extending this type of approach that leverages our knowledge of physics through new models and data augmentation techniques in this dissertation, and apply these approaches to two problems that have limited datasets: the problem of Fluid Flow Velocity Prediction in the field of mechanical engineering and the problem of Glacial Ice Segmentation from geology.
Undergraduate course, University 1, Department, 2014
This is a description of a teaching experience. You can use markdown like any other post.